Getting Started

The easiest way to get started using repliclust is to create synthetic data sets from high-level descriptions in English. Our natural language recognition builds on OpenAI’s API, so using these features requires providing your OpenAI API key. You can set it as OPENAI_API_KEY=<...> in an .env file, or pass it to individual functions as a keyword argument openai_api_key=<...>.

Once the package recognizes your OpenAI key, you generate data directly using the repliclust.generate function. For example,

import repliclust as rpl

X, y, archetype = rpl.generate(
    "seven clusters with very different shapes and different distributions, and mild overlap"
)

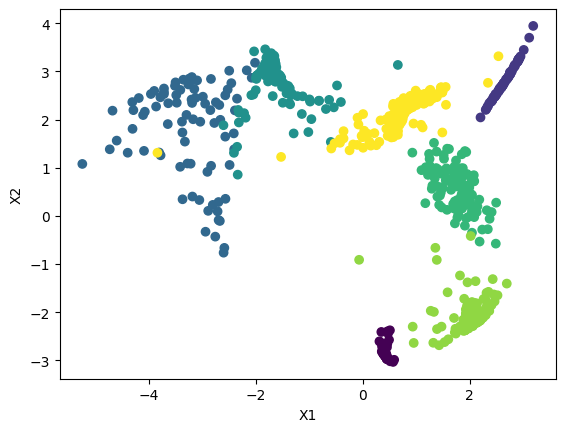
rpl.plot(X, y)

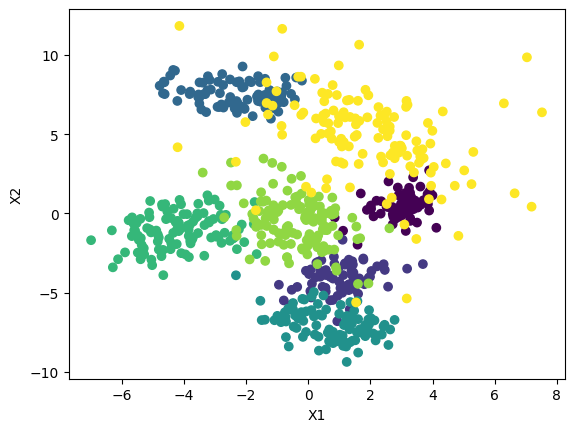
The repliclust.plot function is convenient for creating plots in a notebook environment; it will automatically apply t-SNE (or UMAP) dimensionality reduction if the data has more than two dimensions.

Rather than directly generate data, you can first create an archetype. The Archetype.describe function prints the parameters of your archetype. to understand what these parameters mean, read Specifying an Archetype.

For example, .. code-block:: python

import repliclust as rpl

archetype = rpl.Archetype.from_verbal_description(

“three gamma-distributed clusters in 10D, of which some are long and some are spherical, that are well-separated”

)

archetype.describe()

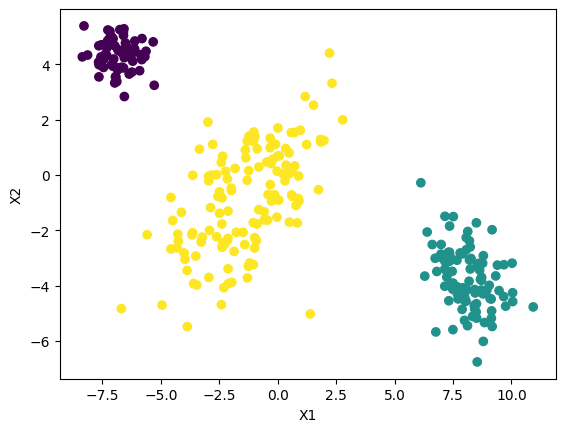
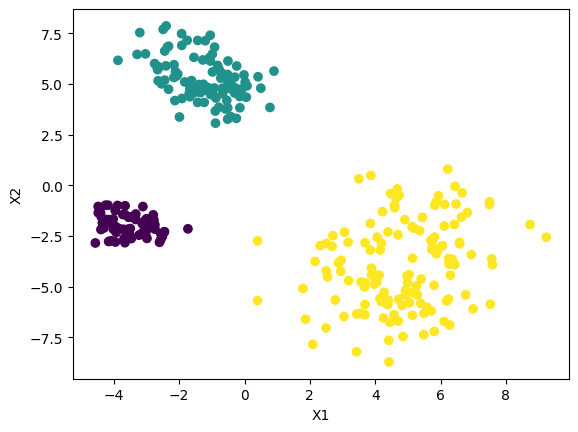
Once an archetype has been defined, you can use it directly to create many different data sets. Continuing our example,

X1, y1 = archetype.synthesize(quiet=True)
X2, y2 = archetype.synthesize(quiet=True)

rpl.plot(X1,y1)
rpl.plot(X2,y2)

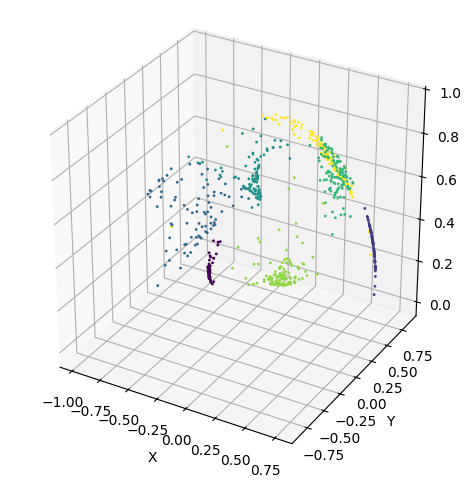
To create irregular cluster shapes, you can use the repliclust.distort and repliclust.wrap_around_sphere functions. The first function creates clusters with irregular shapes by passing data through a randomly initialized neural network. This function may not work properly if you do not have a GPU with CUDA support. The second function wraps a data set around the surface of the sphere. A 2D data set is wrapped around the surface of the three-dimensional sphere, a 3D data set is wrapped around the 4D sphere, etc.

X, y, _ = rpl.generate("seven clusters with very different shapes")
X = rpl.distort(X)

rpl.plot(X,y)

X = rpl.wrap_around_sphere(X)

rpl.plot(X,y)